Hoy me voy a dar el gusto de escribir un artículo que no está 100% relacionado con tecnología. Hace poco decidí entender, de una vez y para siempre, toda la parafernalia de las escalas musicales, el círculo de quintas, las armaduras y el porqué de todo eso.
Siempre me lo habían explicado como memoriza Fa Do Sol Re La Mi Si. Luego memoriza otras 5 reglas (aparentemente) arbirtarias más y ya con eso lo tienes todo. A mí eso no me funciona. La única forma que yo tengo de aprenderme este tipo de cosas es entendiendo por qué suceden. Y, si yo lo pude entender, te garantizo que tú también. Vamos al lío.
Qué es una nota
Y qué son los armónicos
Vamos a intentar empezar por la base. Vamos a explicar qué es una nota y qué son los armónicos, porque eso nos va a poner un cimiento sólido en el conocimiento posterior.
Una nota no es más que una onda oscilando a una frecuencia concreta. La frecuencia más conocida es 440 Hz. Esta frecuencia es el tono de referencia para afinar el La que queda por encima del Do central (quien toque el piano entiende perfectamente esto). Si no sabes qué es el Do central, no hay problema, basta con saber que es el tono de referencia para afinar el La. Pues igual que ese La, todo el resto de notas tiene una frecuencia (igual que cualquier señal).
Los armónicos, por otro lado, son ondas que oscilan a n veces la frecuencia de la fundamental. Espera, ¿qué? No te preocupes, son palabras pomposas para describir algo simple.
La fundamental es la "nota base", los armónicos son las ondas que vibran al doble, triple, cuádruple de la frecuencia de la nota base. Por ejemplo.
| Armónico | Frecuencia (fᵢ) | Herzios | Intervalo |
|---|---|---|---|
| 1 | 1 x f₁ | 440 | Unísono |
| 2 | 2 x f₁ | 880 | Octava |
| 3 | 3 x f₁ | 1320 | Quinta justa |
| 4 | 4 x f₁ | 1760 | Cuarta justa |
| 5 | 5 x f₁ | 2200 | Tercera mayor |
Si viésemos las ondas de los 3 primeros armónicos (fundamental, octava y quinta justa) veríamos algo así:

Si te fijas, puedes ver cómo en el tiempo en el que el azul (la fundamental) hace su único ciclo, el morado (primer armónico) hace 2 y el rosa (tercer armónico) hace 3. Cada ciclo puedes pensarlo como una cresta (máximo) y un valle (mínimo).
Algo no cuadra
Si, como yo, al ver esto te hiciste la pregunta ¿cómo es posible que la quinta, teniendo una frecuencia mayor que la octava, suene más baja? he pensado también en ti. Echa un vistazo a este artículo. Básicamente el cerebro percibe los tonos como una "espiral" y cuando se "encuentra" la octava, la relaciona con la fundamental y "comprime" todo lo que está por medio dejándolo por debajo. Es una explicación estúpidamente simplificada pero que sirve como analogía.
Las relaciones entre frecuencias
Y por qué son cruciales
Vale, ahora que sabes qué son frecuencias y armónicos, vamos a hacer una relación de las frecuencias entre sí, en vez de con la fundamental, porque esto nos va a dar un punto clave en nuestro recorrido.
Vamos a recordar un concepto, por si acaso. Para obtener el ratio entre dos valores, la fórmula sería:
\[ ratio = \frac{\text{valor más alto}}{\text{valor más bajo}} \]
Otra forma de pensarlo es "cuántas veces puedo meter el valor más bajo dentro del más alto".
Si aplicamos esto a nuestras frecuencias, por ejemplo, la fundamental con la octava, sabiendo que \( f_{2} = 2f_{1} \), tenemos
\[ ratio = \frac{2f_{1}}{f_{1}};\quad ratio = \frac{2}{1} \]
Por tanto, solemos decir que la octava tiene una relación de 2:1 con la fundamental. Si aplicamos este mismo cálculo pero en vez de relacionarlo con la fundamental relacionamos a cada armónico con el anterior, nos queda esto:
| Armónico | Frecuencia (fᵢ) | Relación con el armónico anterior | Intervalo |
|---|---|---|---|
| 1 | 1xf₁ | - | Unísono |
| 2 | 2xf₁ | 2:1 | Octava |
| 3 | 3xf₁ | 3:2 | Quinta justa |
| 4 | 4xf₁ | 4:3 | Cuarta justa |
| 5 | 5xf₁ | 5:4 | Tercera mayor |
Vamos a explicar qué significan estas relaciones. La relación 2:1 de la octava con la fundamental significa que cada 2 ciclos de la fundamental, ella y la octava coinciden.
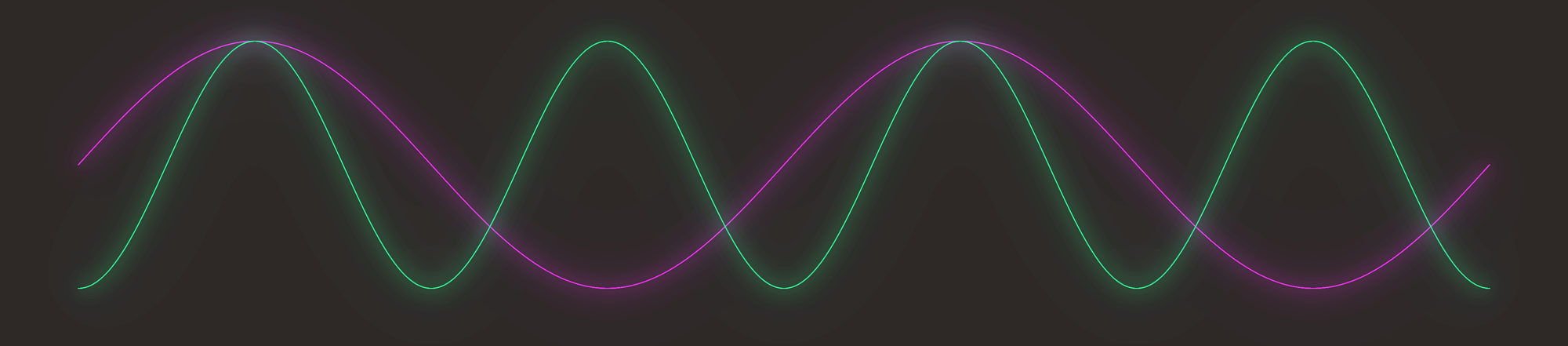
En rosa puedes ver la fundamental y en verde la octava. La octava está desplazada de fase 90 grados para que la visualización sea más cómoda, pero la idea es la misma. Se puede ver que cada dos ciclos, la octava se sincroniza en fase con la fundamental. Esto genera una estabilidad en el oído al percibirla. No hay ningún armónico que se repita con más frecuencia que este (cada dos ciclos). Eso implica que, para una unidad de tiempo, estos dos armónicos son los que se repiten más veces. Por eso se dice que este es el intervalo más estable.
Después tenemos el tercer armónico, el de la quinta justa. En este caso tenemos que, por cada 3 oscilaciones de la más aguda (la quinta), la más grave (la octava) hace 2. Esto podemos verlo en la siguiente imagen.
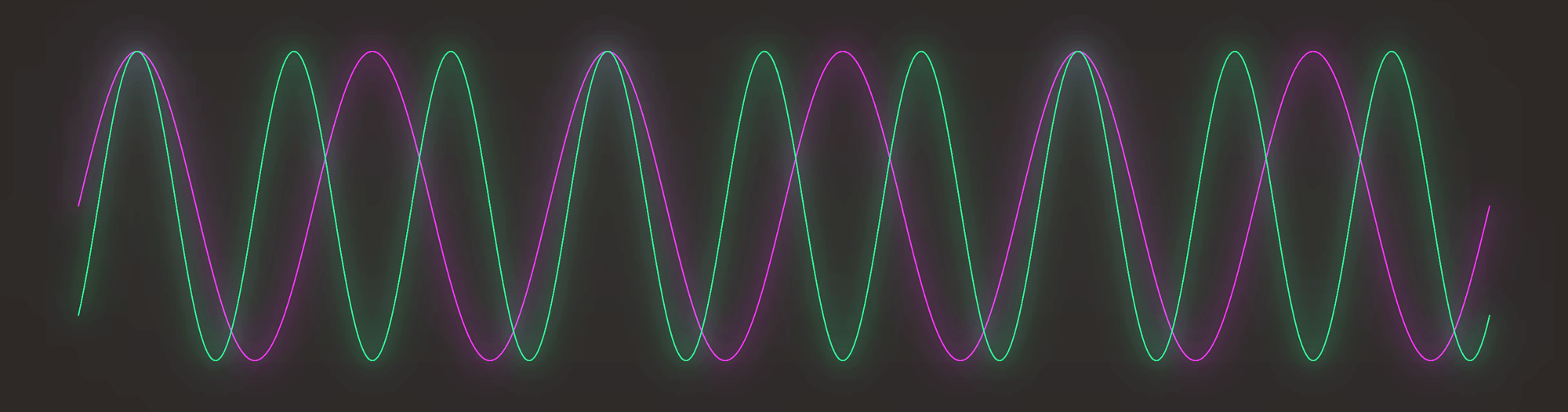
Es similar a la anterior, con la única diferencia de que las coincidencias son cada 3 ciclos en vez de cada dos. Este intervalo es menos estable, pero es el más estable después del de la octava.
Así podríamos seguir con el resto y obtendríamos, cada vez, intervalos más inestables.
Toda esta explicación va a empezar a cobrar sentido ahora mismo, quédate conmigo un poco más, va a merecer la pena.
Dividiendo el espectro auditivo
12 sonidos, 12 semitonos
Ahora vamos a empezar ya con la parte cultural. Vamos a intentar "reconciliar" el intervalo de octava (más estable) con el de quinta (el siguiente más estable). Es decir, vamos a intentar ver cuántos intervalos de quinta podemos meter en el de octava.
Como la octava es el doble de la fundamental y la quinta es \(\frac{3}{2} \) de la octava, necesitamos encontrar dos enteros \( n \) y \( m \) tal que
\[ \left( \frac{3}{2} \right)^n \approx 2^m\]
Esto sería lo mismo que decir que después de haber subido \( n \) quintas, hayas subido \( m \) octavas (conseguir aquí un número entero va a ser complicado, así que hablaremos de subir prácticamente \( m \) octavas).
Esto es lo mismo que decir
\[ \frac{3^n}{2^n} \approx 2^{m}; \quad 3^n \approx 2^{m} \cdot 2^n; \\\ \\\ 3^n \approx 2^{m+n}; \quad \log(3^n) \approx \log(2^{m+n}); \\\ \\\ n\log(3) \approx (m+n)\log(2); \quad \frac{m+n}{n} \approx \frac{\log(3)}{\log(2)} \approx 1.58496... \]
Aquí nos topamos con un problema, porque tenemos \( \log_2{3} \) (que, en palabras, sería precisamente cuántas octavas caben en una quinta). Esto es un problema porque el resultado de ese logaritmo es un número irracional, es decir, un número que no se puede expresar como una división entre otros dos. Esto implica que no existen 2 números \(n\) y \(m\) que te vayan a dar el resultado que buscamos. La única alternativa que nos queda es intentar aproximar esa fracción.
Decir que \( \frac{m+n}{n} \approx \frac{\log(3)}{\log(2)} \) es lo mismo que decir que \( \frac{m}{n} \approx \log_{2}(3) - 1 \). Si dejamos aparte este desplazamiento de una unidad (podemos volver a aplicarlo luego), necesitamos aproximar \( \frac{m}{n} \) al número irracional \( 1.58496... \).
Para aproximar este tipo de números se puede usar una cosa llamada fracción continua, pero vamos a dejarlo fuera de este artículo, porque no tiene sentido meternos ahí. Lo que nos interesa es ver qué aproximaciones salen. Vamos a verlas en esta tabla:
| m (octavas) | n (quintas) | m/n | Porcentaje de error |
|---|---|---|---|
| 1 | 1 | 1.000 | 27.09% (altísimo) |
| 3 | 2 | 1.500 | 5.3% |
| 8 | 5 | 1.600 | 0.94% |
| 19 | 12 | 1.583 | 0.10% |
| 65 | 41 | 1.585 | 0.02% |
Hay dos filas muy interesantes, con un error muy bajo. La que dice que en 12 quintas caben 19 octavas y la que dice que en 41 quintas caben 65 octavas. A pesar de que la última tiene un error muy bajo, los números son tan altos que los hace muy poco prácticos para trabajar con ellos. Vamos a ver qué pasa si asumimos \( m=19 \) y \( n=12 \).
Esto implica decir que cada 12 quintas, tenemos 19 octavas. Una relación que no te da ningún otro número más pequeño y con un margen de error tan bajo. Si decimos que dividimos cada "vuelta" en 12 pasos (12 quintas), 19 octavas serían 7 pasos (cada vez que llegas al 12 vuelves a empezar en 1, \(19 \mod 7 \)). Y esto respondería a la pregunta inicial
\[ \left( \frac{3}{2} \right)^n \approx 2^m\]
¿Cuántas veces tengo que multiplicar \(\frac{3}{2}\) por sí mismo (cuántas quintas debo subir) para llegar a un número de octavas casi idéntico? La respuesta es 12 quintas, para llegar a 7 octavas. Si sustituimos valores:
\[ \left( \frac{3}{2} \right)^{12} \approx 2^7 \quad 129.746 = 128 \]
Y justo esa diferencia, ese 1.746 es lo que se conoce como la coma pitagórica.
Pero ahora mismo no nos vamos a preocupar de eso (aunque es un tema interesantísimo). ¡Ahora lo que no interesa es que hemos dividido nuestra nuestro intervalo desde una frecuencia hasta su octava en 12 partes iguales! Pero esto nos viene con un añadido. Si hemos dividido en 12, sabemos que la relación de la quinta en este sistema tiene que ser 7 pasos. Luego volveremos al amado 7 y veremos por qué.
El círculo de quintas
La explicación matemática
Bien, ya tenemos nuestro sistema dividido en 12 pasos. Ahora vamos a darle nombre, el nombre que conocemos todos, el nombre de las doce notas (contando alteraciones).
Do Do# Re Re# Mi Fa Fa# Sol Sol# La La# Si
Cada vez que repites esos 12 sonidos en orden, vuelves al inicial subiendo 1 octava, todo cuadra con lo que hemos visto hasta ahora. A partir de ahora vamos a hablar del sistema de notas como un sistema en módulo 12. Esto es que cada vez que llegas al 11 (Si) vuelves al 0 (Do).
Para recorrer todos los valores de un sistema en un módulo \( n \) lo que se debe hacer es ir sumando un número \( m \) tal que \( m \) y \( n \) sean coprimos. Dos números son coprimos si no tienen ningún divisor en común salvo el 1. Como estamos en módulo 12, además sabemos que \( 1 \le m \le 12 \). No hay muchos números, si empezamos a comprobar, el 1 es coprimo con el 12, porque solo comparten el 1 como divisor. De hecho, si vamos sumando 1, efectivamente generamos todos los valores del sistema, y en orden (1, 2, 3, 4...). El 2 no es coprimo con el 12 porque comparten tanto el 2 como el 1 como divisores. Si comprobamos todos, tenemos que los coprimos con el 12 son el 1, 5, 7 y 11. El 7. El amado 7 vuelve a aparecer. Vamos a ver en qué orden recorre los valores del sistema.
| Posición | +7 | mod 12 | Nota |
|---|---|---|---|
| 0 | - | 0 | Do |
| 0 | 7 | 7 | Sol |
| 7 | 14 | 2 | Re |
| 2 | 9 | 9 | La |
| 9 | 16 | 4 | Mi |
| 4 | 11 | 11 | Si |
| 11 | 18 | 6 | Fa# |
| 6 | 13 | 1 | Do# |
| 1 | 8 | 8 | Sol# |
| 8 | 15 | 3 | Re# |
| 3 | 10 | 10 | La# |
| 10 | 17 | 5 | Fa |
Recorre todos los valores del sistema. Además, los recorre en un orden muy bonito, primero los naturales y luego, en el mismo orden, las alteraciones. Si empezamos a contar desde el último, desde el Fa, nos queda Fa, Do, Sol, Re, La, Mi, Si... ¿Te suena? ¡Acabamos de construir el círculo de quintas!
En nuestro sistema, cada "paso" es un semitono, ir subiendo de 7 en 7 significa subir 3 tonos y medio cada vez, una quinta.
¿Y si bajamos?
Desentrañando las cuartas
Una cosa que se aprende siempre es que si coges el círculo de quinta y lo recorres hacia abajo (Si Mi La Re Sol Do Fa), estás bajando cuartas, bajas 2.5 tonos cada vez. Vamos a ver por qué pasa esto.
De lo primero que te habrás dado cuenta es que 2.5 tonos son 5 semitonos y que, como vimos arriba, 5 es coprimo con 12. Así que tiene todo el sentido del mundo que al recorrer en cuartas también generes todos los valores posibles. Vamos a montar la misma tabla anterior pero con cuartas.
| Posición | +5 | mod 12 | Nota |
|---|---|---|---|
| 1 | - | 1 | Do |
| 1 | 6 | 6 | Fa |
| 6 | 5 | 11 | La# |
| 11 | 16 | 4 | Re# |
| 4 | 9 | 9 | Sol# |
| 9 | 14 | 2 | Do# |
| 2 | 7 | 7 | Fa# |
| 7 | 12 | 12 | Si |
| 12 | 17 | 5 | Mi |
| 5 | 10 | 10 | La |
| 10 | 15 | 3 | Re |
| 3 | 8 | 8 | Sol |
Si empezamos a contar desde que terminan las alteraciones tenemos Si Mi La Re Sol Do Fa. ¡Exactamente el círculo de quintas pero a la inversa! ¿Por qué pasa esto?
Vamos a verlo. En módulo \( M \), dos números son equivalentes si su diferencia es múltiplo de \( M \). Por ejemplo, para módulo 12, si tomamos el número 6 y el 18. La diferencia entre ellos es 12, ¿es múltiplo de 12? Sí, pues en módulo 12 son equivalentes. Efectivamente \( 18 \mod 12 = 6 = 6 \mod 12 \). Por eso en un reloj, las 18 y las 6 son equivalentes (misma posición). Esta condición en lenguaje matemático se expresa como
\[ a \equiv b (\mod M) \iff M \mid (a-b) \]
Y, por otro lado, cuando tú haces el módulo \( M \) de un número \( a \) , en realidad lo que estás haciendo es dividir \( a \) entre \( M \) y quedarte con el resto. Eso se puede explicar así
\[ a = q \cdot M + r \quad \text{tal que} \quad 0 \leq r \le M \]
Es decir, que para sacar \( a \mod M \) tenemos que encontrar un número \( q \) que multiplique a \( M \) (cuántas veces cabe \( a \) en \( M \)) y un número \( r \) que sumándolo (cuántos sobran) nos dé \( a \). Además sabemos que \( r \) siempre va a estar entre \( 0 \) (división exacta) y \( M - 1 \).
Por ejemplo, vamos a intentar hallar \( 32 \mod 12 \), necesitamos cumplir
\[ 32 = q \cdot 12 + r \]
Sabemos que el 32 cabe 2 veces en 12 (3 veces ya son 36), así que
\[ 32 = 2 \cdot 12 + r; \quad 32 = 24 + r \\\ r = 8 \]
¡Perfecto! entonces \( 32 mod 12 = 8 \). Sabiendo esto, vamos a ver qué pasa si intentamos hacer \( -7 mod 12 \), que es lo que hacemos al bajar en el círculo de quintas (1 quinta, 7 semitonos, bajar una quinta, bajar 7 semitonos). Sabemos que estamos buscando
\[ -7 = q \cdot 12 + r \]
Pero sabemos que \( r \) debe ser positivo y menor a 12. Si \( q = 0 \), \( r = -7 \), si \( q = 1 \), \( r = -19 \), mientras más alto \( q \), más pequeño \( r \), vamos a probar en la otra dirección.
\[ -7 = -1 \cdot 12 + r; \quad -7 = -12 + r \\\ r = 5 \]
¿Cómo? \( -7 \mod 12 = 5 \). ¡¡Bajar 7 semitonos es lo mismo que subir 5!! Pero, si te das cuenta de lo que ha pasado, lo que hemos hecho para sacar \( r \) ha sido restar nuestro paso negativo a \( M \). Es decir, que lo que estamos diciendo es que \( -n \mod M = M - n \). ¿Esto es verdad? Bueno, dijimos antes que dos números en un módulo concreto eran equivalentes si su diferencia era múltimo del módulo, así que vamos a probar a restar entre sí \( -n \) y \( M - n \) a ver qué pasa.
\[ -n - (M - n) = -n - M + n = -M \]
Resulta que si los restamos entre sí lo que obtenemos es \( -M \), ¿es \( -M \) múltiplo de \( M \)? Por supuesto que sí. Por eso, en general, para cualquier sistema modular en \( M \) podemos decir:
\[ \text{La inversa de sumar }n\text{ es }M - n\quad n \equiv (M-n) \mod M \]
Por eso, al bajar por el círculo de quintas (bajar 7 semitonos) lo que estamos haciendo en realidad es subir cuartas (subir 5 semitonos).
Quédate un poquito más que solo nos queda una última cosa por ver.
Las alteraciones
Y cómo saber una tonalidad con la armadura
Esta última parte es la que conecta todo y lo pone a trabajar, la que te zarandea el cerebro y hace que no olvides esto jamás. Por qué podemos usar el círculo de quintas para conocer las alteraciones de una escala concreta.
Vamos a poner aquí los intervalos de una escala mayor:
T T S T T T S
Si esto lo cambiamos por el número de pasos de nuestro sistema (1 tono, 2 semitonos, 2 pasos):
2 2 1 2 2 2 1
Vamos a ver qué pasa si cogemos esa progresión de intervalos y los movemos una quinta hacia arriba. Sabemos que una quinta son 7 pasos, tenemos que cortar cuando nuestros intervalos sumen 7. En nuestro caso, cortamos en el tercer 2. Y ahora comenzamos a colocar los intervalos que hemos cortado, pero comenzando desde el corte. Vamos a verlo en una representación visual.
Como puedes ver, la escala se queda descuadrada, quedan 2 intervalos intercambiados al final. ¿Cómo podemos solucionarlo? Necesitamos que el 1 final sea un 2 y que el 2 final sea un 1. Si piensas en el significado, necesitamos que en el penúltimo paso haya un tono en vez de un semitono y en el último un semitono en vez de un tono. Esto es tan sencillo como sumar un semitono a la penúltima, eso hace automáticamente que tenga un tono completo con la anterior y, por tanto, medio tono con la siguiente.
Esto significa que, una vez que añadimos 1 alteración, la escala vuelve a quedar redonda. Entonces, si volvemos a subir 1 quinta, partimos de la situación "estable" (con 1 alteración) y tenemos que añadir 1 corrección más, ya van dos alteraciones. Si sigues así, vas teniendo exactamente 1 alteración nueva por cada quinta que subas.
La representación visual está muy bien, pero vamos a ver qué pasa en nuestro sistema.
Tenemos que con la secuencia 2 2 1 2 2 2 1 los semitonos caen en las posiciones 3-4 y 7-8, pero nosotros estamos en un sistema de 12 sonidos, lo que nos interesa es saber en qué posiciones de ese sistema de 12 están, vamos a construir la escala de Do muy rápido.
| Nota | Posición (mod 12) |
|---|---|
| Do | 0 |
| Re | 2 |
| Mi | 4 |
| Fa | 5 |
| Sol | 7 |
| La | 9 |
| Si | 11 |
| Do | 12 ≡ 0 |
Si te fijas, los semitonos están entre las notas en la posición 4-5 (Mi Fa) y las notas en la posición 11-0 (Si Do). Vamos a hacer la escala de la nota que está una quinta sobre Do (una quinta 7 semitonos, 7 semitonos de Do es Sol), vamos a hacer la escala de Sol pero símplemente tomando la de Do y sumando 7 a cada posición (y aplicando módulo 12):
| Nota (en escala de Do) | Posición (en escala de Do) | Nueva posición (+7 mod 12) | Nota (en escala de Sol) |
|---|---|---|---|
| Do | 0 | 7 | Sol |
| Re | 2 | 9 | La |
| Mi | 4 | 11 | Si |
| Fa | 5 | 0 | Do |
| Sol | 7 | 2 | Re |
| La | 9 | 4 | Mi |
| Si | 11 | 6 | Fa# |
| Do | 12 ≡ 0 | 7 | Sol |
Al hacer la escala, automáticamente aparece una alteración, el Fa#. Si tomamos los intervalos de los semitonos en la escala de Do (4-5 y 11-0) y les sumamos una quinta, nos queda 11-12 y 18-19 (recuerda que \( 0 \mod 12 \) es 12). Aplicando módulo 12 a ambos nos quedan 11-0 y 6-7. Es muy curioso, porque el que antes era 4-5 (Mi Fa) ha pasado a ser 11-0 (Si Do) que se ha movido de posición. El otro se ha desplazado a 6-7, que es la corrección que hacíamos antes de +1 en el vídeo.
Si seguimos haciendo este desplazamiento por quintas, 11-0 vuelve a pasar a 6-7 (la alteración que ya teníamos en la escala de Sol), y 6-7 pasa a ser 13-14, que módulo 12 es 1-2 y es la nueva alteración que nos aparece, la nota en la posición 1 de nuestra escala es Do#.
Si repetimos esto, como estamos recorriendo el círculo de quintas sumando 7 (recuerda, coprimo con 12), cada vez que subas una quinta te va a aparecer exactamente una alteración nueva y ¡justo será la siguiente nota en el círculo de quintas!
Entonces, si tú quieres saber cuántas alteraciones tiene, por ejemplo, la escala de Re, lo que tienes que preguntarte es
¿Cuántas quintas desde Do he tenido que desplazarme para llegar a Re?
Si el círculo de quintas es Fa Do Sol Re La Mi Si, desde Do (que no desde Fa) has tenido que subir 2 quintas, por tanto, la escala de Re tiene 2 alteraciones. Ahora, la segunda pregunta
¿Qué alteraciones tiene la escala de Re?
Pues, como sabemos que las alteraciones aparecen en el orden del círculo de quintas, 2 alteraciones empezando por la primera que aparece del círculo (que es Fa), las alteraciones serán Fa y Do, por tanto, llegamos a la conclusión de que la escala de Re tiene que ser Re Mi Fa# Sol La Si Do#. Increíble.
Y para bajar pasa exactamente lo mismo, cuando bajas una cuarta (recuerda que era sumar 5), los intervalos 4-5 y 11-0 quedan como 9-10 y 16-17. Aplicando módulo 12 nos queda 9-10 y 4-5. ¡Exactamente igual! Un intervalo se mantiene pero en otra posición de la escala y el otro sufre un ajuste. ¡El ajuste es precisamente la primera nota del círculo de quintas si empiezas a la inversa! Si Mi La Re Sol Do Fa.
Por eso para montar la escala de Fa no tiene sentido que mires cuántas quintas subes desde Do porque teniendo Fa Do Sol Re La Mi Si es mucho más rápido decir que bajas 1 quinta o, lo que es lo mismo, subes una cuarta. Como subes 1 cuarta desde Do, en el círculo de quintas inverso Si Mi La Re Sol Do Fa, la primera alteración que aparece es Si (bemol si hablamos de bajar 1 cuarta, La# si hablamos de subir una quinta), y la escala de Fa es, por tanto, Fa Sol La La# Do Re Mi Fa. Si queremos hacerlo bien, sin repetir notas, Fa Sol La Sib Do Re Mi Fa.
¡Ahora sí que sí lo tenemos todo!
Imagina que te encuentras esto en una armadura:
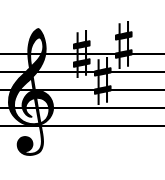
Esto te está diciendo:
Para saber la tonalidad de esta partitura, te digo que hemos subido 3 quintas desde 2.
Con eso ya lo tienes todo.
Fa Do Sol Re La Mi Si
0 1 2 3
Desde Do, subir 3 quintas es llegar a La. Pues ya sabes que esa partitura está en La (también puede estar en su relativo menor, pero esa historia es para otro artículo).
Y ahora, ¿cuáles son las alteraciones de la escala de La? Pues las 3 primeras del círculo de quintas. Fa, Do, Sol.
Y para bemoles lo mismo. Si tienes dos bemoles, la pregunta es
¿En qué nota estoy si he bajado dos cuartas desde Do?
Teniendo Si Mi La Re Sol Do Fa, contando dos cuartas hacia abajo desde Do (recuerda que esa escala ya está descendente, así que tienes que subir), acabas en Si. Por lo que estarías en la tonalidad de Sib mayor (de nuevo, ignoramos aquí el relativo menor).
Y, de nuevo, queda la segunda pregunta.
¿Qué alteraciones tiene la escala?
Pues tomando el mismo círculo de cuartas y empezando, ahora sí, desde Si, nos quedan Sib y Mib. Por tanto la escala que queda es Sib Do Re Mib Fa Sol La Sib.
Enhorabuena, te has convertido en máster de tonalidades, armaduras, escalas y quintas.
Sé que el artículo ha sido durísimo, pero espero que se haya entendido todo y esté todo bien claro.
Cualquier pregunta, duda o sugerencia, me puedes escribir por Twitter @ElAleSM o por mail a hi@alesanchez.es
